Chapter13.3: Floating-point numbers,Representation and Manipulation

Format
What are the effect of decreasing the number of bits allocated to Mantissa and increasing the exponent
- Reduction in precision
- As the number of bits in mantissa has decreased.
- Increasing in range
- As the number of bits in exponent has increased.
The denary number 513 cannot be stored accurately as normalised floating-point number in this computer system: (10 bits for mantissa, 6 bits for exponent)
Explain reasons for this:
- Require more than 10 bits/11bits to store; the maximum number that can be stored is 511
- The denary 513 in binary is 1000000001 // Normalised: 0.1000000001
- Results in overflow
Describe an alteration to the way floating-point numbers are stored to enable this number to be stored accurately with the same total number of bits:
- The number of bits for mantissa must be increased
- 11 bits for mantissa and 5 bits for exponent
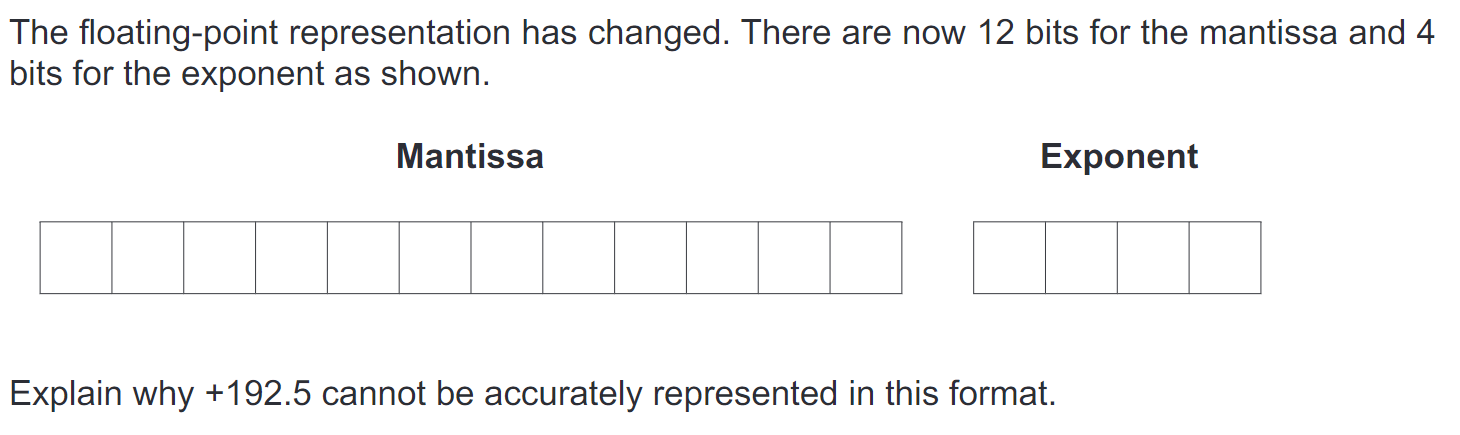
- Exponent too large to fit 4 bits as two’s complement number
- Exponent will turn negative
- … therefore the binary point moves the wrong way
- Value will be approximately +0.029(296875)
Explain the trade-off between either using a large number of bits for the mantissa, or a large number of bits for the exponent
- The trade-off is between range and precision
- Any increase in the number of bits for the mantissa means fewer number of bits for the exponent
- More bits used in mantissa would result in better precision
- More bits used in exponent would result in larger range
Conversion
Calculate the normalised binary number for -3.75. Show your working
- -3.75 = 100.01000 // -4 + 1/4 // -4 + 0.25
- 100.01000 becomes 1.0001000 Exponent=+2
- Answer: Mantissa=1.0001000 Exponent=0010
Calculate the normalised floating-point representation of +1.5625 in this system (12bit-mantissa, 4bit-exponent). Show your working
- Correct conversion to binary: 01.1001
- Correct calculation of the exponent: 1
- Answer: Mantissa=0110 0100 0000 | Exponent= 0001
Normalisation
Why binary/floating-point numbers are stored in normalized form
- To store the maximum range of numbers in the minimum number of bits
- Normalisation minimizes the number of leading zeros/ones represented
- Maximizing the number of significant bits // maximizing the number of precision/accuracy with given number of bits
- Enable large/small numbers to be stored with accuracy
- Avoids the possibility that many numbers have multiple representation
--- There will be a unique representation for a number
- The format will ensure it will be represented with greatest possible accuracy
- Multiplication is performed more accurately
Problems that can occur when a floating-pointer number is not normalised
- Lost of precision
- Redundant leading zeros in the mantissa
- Lost of the least-significant bits (bits on the right-hand end)
- Multiple representation of a single number
Approximation & Rounding errors
State why some binary representation can lead to rounding errors
- There’s no exact binary conversion for some numbers
- More bits are needed to store the number


- 0.2 and 0.4 cannot be represented exactly in binary, there is a rounding error
- 0.2 has been represented by a number just greater than 0.2
- This is similar for 0.4
- Therefore, multiplying these two representations together increases the difference
- Difference after calculation is significant enough to be seen

- 0.1 cannot be represented exactly in binary, there is a rounding error
- 0.1 is represented by a value just less than 0.1
- The loop keeps adding this approximate value to the counter
- Until all accumulated small difference become significant enough to be seen